Laskentaohjelmalla oppii uutta

Laskin Mathematica-ohjelmistolla Fourier'n sarjaa funktiolle $f(x) = x$ välillä $[-\pi,\pi]$. Tuloksena on
\[
\sum_{n=1}^{\infty} \frac{2(-1)^{n+1}}{n}\,\sin(nx) =
2\sin(x) - \sin(2x) + \frac{2}{3}\sin(3x) - \frac{1}{2}\sin(4x) + \dots ,
\]
kuten eri kurssien harjoitustehtävänä on lukuisia kertoja laskettu.

Sarjan summa $s(x)$ on paloittain jatkuva funktio, joka avoimella välillä $]-\pi,\pi[$ saa arvot lausekkeen $f(x) = x$ mukaisesti, välin päätepisteissä arvon $0$ ja joka jatketaan jaksollisesti koko reaaliakselille. Funktio ei siten ole jatkuva pisteissä $\pi + 2n\pi$, $n$ kokonaisluku. Kuvaaja näyttää alla olevan kuvan mukaiselta.

Mathematicahan osaa summeerata kaikenlaista, joten ajattelin kokeilla, antaako se sarjan summaksi jollakin tavoin esitetyn paloittain jatkuvan funktion. Tulos hieman yllätti:
\[
s(x) = i\left(\log(e^{-ix}(1+e^{ix})) - \log(1+e^{ix})\right).
\]
Kompleksialueen funktioita siis, eksponentti- ja logaritmifunktio, ja tuloksen pitäisi kuitenkin olla reaalinen. Epäjatkuvuuksiakin pitäisi olla.

Helpointa on lähteä katsomaan asiaa piirtämällä kuvaaja. Tämä toki ei ole todiste, mutta näyttää ainakin, onko edes mahdollista, että lauseke olisi oikein. Tuloksena on tällöin juuri sellainen kuvaaja kuin pitäisikin.

Seuraavaksi kuvaaja lausekkeen imaginaariosasta:

Hieman hyppii, mutta pystyakselin yksiköt ovat luokkaa $10^{-16}$, joka vastaa Mathematican grafiikan laskentatarkkuutta. Imaginaariosa näyttäisi siis olevan identtisesti $= 0$, joten hyvältä näyttää.

Saatua funktiota $s(x)$ voi katsoa myös kompleksitason funktiona, ts. sijoittaa $x = u + iv$ ja piirtää funktion reaali- ja imaginaariosan kuvaajat kahden muuttujan ($u$ ja $v$) funktioina. Sama koskee funktion itseisarvoa $|s(x)|$.

Reaaliosa

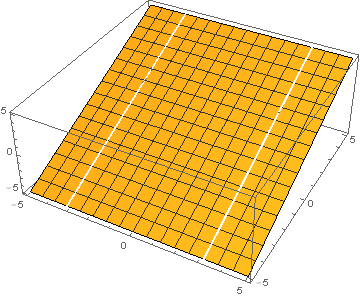Imaginaariosa

Itseisarvo

Näiden merkityksen pohtiminen on jo hieman vaativampaa.

Miten sitten funktion lausekkeesta voi syntyä epäjatkuvuuksia? Avaimena on kompleksisen logaritmifunktion ymmärtäminen:
\[
\log z = \log|z| + i \arg z + 2n\pi i,
\]
missä $n$ on kokonaisluku ja arvo $n = 0$ antaa ns. päähaaran. (Kyseessä on luonnollisen logaritmin laajennus, mutta kompleksialueella ei yleensä käytetä lyhennettä $\ln$.)

Napakulma eli argumentti $\arg z$ saa päähaaralla arvot väliltä $]-\pi,\pi]$, jolloin rajakohtaa $\arg z = \pi$ ohitettaessa syntyy hyppy suuruudeltaan $2\pi$.  Tämä synnyttää epäjatkuvuudet.

Kompleksista logaritmifunktiota voi tutkia piirtämällä kuvaajia sen päähaarasta kahden muuttujan funktiona $\log(u + iv)$. Alla on nähtävissä kolme: reaaliosa, imaginaariosa ja reaaliosa väritettynä imaginaariosan mukaisesti. Hyppyepäjatkuvuus näkyy kahdessa jälkimmäisessä pinnan repeämänä ja ja värin äkillisenä vaihtumisena.

Reaaliosa

Imaginaariosa

Reaaliosan kuvaaja, väritys imaginaariosan mukaan 

Mathematica on siis summeerannut aivan oikein. En vain ole koskaan tullut ajatelleeksi, että epäjatkuvuuksia voisi toisinaan käsitellä myös näin. Tarpeettoman kryptinen tapa selvän asian esittämiseen tämä kyllä saattaa olla.

Kompleksifunktioiden alkeista tarkemmin kiinnostunut lukija voi silmäillä dokumenttia http://matta.hut.fi/matta/kompleksiluvut/cluvut.pdf.