Leonardo Pisalainen (noin 1170-1250) tunnetaan paremmin nimellä Fibonacci. Nimi on lyhentymä ilmaisusta filius Bonacci, Bonaccin poika, jossa Bonacci viittaa sukuun eikä isään. Hänet tiedetään lähinnä nimeään kantavasta lukujonosta, mutta Fibonacci oli paljon monipuolisempi matemaatikko. Vuonna 1202 ilmestyneessä teoksessaan Liber abaci ('laskemisen kirja') hän esittelee intialais-arabialaisen lukujärjestelmän, ts. meidän käyttämämme kymmenkantaisen paikkajärjestelmän (ykköset oikealla, kymmenet seuraavaksi vasemmalla, sitten sadat jne.), jonka käyttö alkoi tuohon aikaan vähitellen levitä Eurooppaan. Kesti kuitenkin nelisensataa vuotta, ennen kuin järjestelmä kaikkine desimaalilukumerkintöineen vakiintui. Tämän ohella Liber abaci käsittelee kaupankäynnin matematiikkaa, erilaisia matemaattisia probleemoja sekä geometriaan ja lukuteoriaan luettavia konstruktioita. Muutama muukin Fibonaccin teos on säilynyt.
Liber abacin probleemojen joukossa on myös kanien lisääntymistä koskeva tehtävä: Kanipari pannaan suljettuun aitaukseen. Ne synnyttävät joka kuukausi uuden parin. Nämä ovat kuukauden kuluttua sukukypsiä ja synnyttävät uuden parin jne. Kuinka monta paria aitauksessa on vuoden kuluttua? Fibonacci osoittaa, että kuukausittaiset määrät ovat $1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233$ ja vuoden kuluttua $377$. Yllä olevassa kuvassa Fibonaccin alkuperäinen teksti; määrät laskettu oikeassa reunassa.
Syntyvää lukujonoa on alettu kutsua Fibonaccin luvuiksi. Ne määritellään usein rekursiivisesti: \[f(0)=0,\ f(1)=1,\ f(n)=f(n-1)+f(n-2),\ n \ge 2.\] Seuraava luku on siis aina kahden edellisen luvun summa: \[0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,\dots\] Kaniparien lukumäärät alkavat luvusta $f(2)$. Kanien lisääntymisen ohella Fibonaccin luvuilla on osoittautunut olevan yhteys moneen asiaan. Tunnetuin lienee kultaisen leikkauksen suhde, jota peräkkäisten Fibonaccin lukujen suhde lähestyy. Hieman erikoisempana esimerkkinä olkoon istumajärjestysongelma: Tuolirivissä on $n$ tuolia ja siihen sijoitetaan kahdenlaisia ihmisiä, rauhallisia ja herkästi riitaantuvia, joita ei voida sijoittaa rinnakkain. Kuinka monella tavalla tuolirivi voidaan täyttää? Vastauksena on Fibonaccin luku. (Esimerkki on peräisin Ron Knottin dokumentista.)
Hakukone löytää lisää verkkodokumentteja Fibonaccin luvuista. Lähtökohtana voi myös käyttää kanadalaisen Fibonacci Associationin sivua tai edellä mainitun Ron Knottin sivua.
Rekursiivisen määrittelyn sijaan Fibonaccin lukuja voidaan tarkastella myös eksplisiittisesti: $f(n)$ lausekkeena, joka riippuu indeksistä $n$. Rekursiokaavaa $f(n)=f(n-1)+f(n-2)$ ajatellaan tällöin ns. differenssiyhtälönä, jolle etsitään ratkaisu. Menettely on samankaltainen kuin lineaarisen vakiokertoimisen differentiaaliyhtälön ratkaiseminen: muodostetaan sopiva yrite, jossa on tuntematon symboli, ja pyritään määrittämään tämä. Osoittautuu, että yritteeksi kannattaa valita $f(n) = r^n$ ja pyrkiä määrittämään $r$. Kun yrite sijoitetaan differenssiyhtälöön, saadaan \[r^n = r^{n-1} + r^{n-2}.\] Kun tämä jaetaan potenssilla $r^{n-2}$, saadaan luvulle $r$ toisen asteen yhtälö \[r^2 = r + 1.\] Tällä on kaksi juurta: $r_1 = \frac{1}{2}(1 + \sqrt{5})$ ja $r_2 = \frac{1}{2}(1 - \sqrt{5})$. Differenssiyhtälöllä on siis ratkaisuna potenssit $r_1^n$ ja $r_2^n$. Mutta sijoittamalla differenssiyhtälöön todetaan, että sillä on ratkaisuna myös jokainen lauseke $f(n) = c_1 r_1^n + c_2 r_2^n$, missä $c_1$ ja $c_2$ ovat mitä tahansa vakioita (so. riippumattomia luvusta $n$). (Tähän viitataan sanomalla, että differenssiyhtälö on lineaarinen.)
Fibonaccin luvuilla on lisäksi ominaisuudet $f(0) = 0$, $f(1) = 1$. Nämä ovat differenssiyhtälön kannalta ns. alkuehtoja, ja niistä seuraa yhtälöt $c_1 + c_2 = 0$, $c_1r_1 + c_2r_2 = 1$. Tällöin $c_1 = -c_2 = \frac{1}{\sqrt{5}}$ ja Fibonaccin luvun lausekkeeksi saadaan \[f(n) = \frac{1}{\sqrt{5}}\biggl(\Bigl(\frac{1 + \sqrt{5}}{2}\Bigr)^n - \Bigl(\frac{1 - \sqrt{5}}{2}\Bigr)^n\biggr).\]
Luku $r_1$ on itse asiassa kultaisen leikkauksen suhde. Tässä jana jaetaan kahteen osaan, pituuksiltaan $a$ ja $b$ ($a > b$). Näiden suhde $q = a/b$ on kultaisen leikkauksen suhde, jos pidemmän osan suhde lyhyempään on sama kuin koko janan suhde pitempään, ts. \[\frac{a}{b} = \frac{a+b}{a}.\] Tämä johtaa yhtälöön $q^2 = q + 1$, jonka positiiviseksi juureksi edellä todettiin $q = r_1 = \frac{1}{2}(1 + \sqrt{5})$. Negatiivinen juuri on $r_2 = \frac{1}{2}(1 - \sqrt{5}) = -1/q$.
Eksplisiittisen lausekkeen avulla nähdään, että Fibonaccin lukujen suhde $f(n+1)/f(n)$ lähestyy kultaisen leikkauksen suhdetta, kun $n$ lähestyy ääretöntä.
Fibonaccin luvut toteuttavat koko joukon erilaisia algebrallisia identiteettejä. Kokeilemalla voi todeta, että esimerkiksi lauseke $f(n)f(m) + f(n+1)f(m+1)$ antaa aina jonkin Fibonaccin luvun. Esimerkiksi arvoilla $n=6$, $m=9$ saadaan $8 \cdot 34 + 13 \cdot 55 = 987$. Saattaa olla hieman vaikeata todistaa rekursiokaavan avulla, että näin todella on (en ainakaan nopeasti löytänyt todistusta), mutta eksplisiittisen lausekkeen avulla se on suora lasku: \begin{align*}&f(n)f(m) + f(n+1)f(m+1)\\ &= \tfrac{1}{5}(r_1^n - r_2^n)(r_1^m - r_2^m) + \tfrac{1}{5}(r_1^{n+1} - r_2^{n+1})(r_1^{m+1} - r_2^{m+1})\\ &= \tfrac{1}{5}(r_1^{n+m} + r_2^{n+m} - r_1^nr_2^m - r_2^nr_1^m + r_1^{n+m+2} + r_2^{n+m+2} - r_1^{n+1}r_2^{m+1} - r_2^{n+1}r_1^{m+1})\\ &= \tfrac{1}{5}(r_1^{n+m}(1+r_1^2) + r_2^{n+m}(1+r_2^2) - (r_1^nr_2^m + r_2^nr_1^m)(1 + r_1r_2)).\end{align*} Koska \[1+r_1^2 = \tfrac{1}{2}(5+\sqrt{5}) = \sqrt{5}r_1, \quad 1+r_2^2 = \tfrac{1}{2}(5-\sqrt{5}) = -\sqrt{5}r_2, \quad 1+r_1r_2 = 0,\] tämä saadaan muotoon \[\frac{1}{\sqrt{5}}\left(r_1^{n+m+1} - r_2^{n+m+1}\right) = f(n+m+1).\] Esimerkissä on siten $987 = f(6+9+1) = f(16)$.
Jos tulos on tiedossa tai kokeilujen perusteella arvattu, niin todistamisessa tarvittava mekaaninen lasku sujuu vaivatta symbolisella laskentaohjelmalla (alla käytetty Mathematicaa ja GeoGebraa):
Fibonaccin luvuista ja niitä koskevista identiteeteistä on laaja artikkeli Wolfram MathWorld -sivustossa.

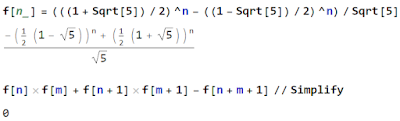

Ei kommentteja:
Lähetä kommentti